[Python] 백준 18352 특정 거리의 도시 찾기 (Dijkstra)


📌 문제
어떤 나라에는 1번부터 N번까지의 도시와 M개의 단방향 도로가 존재한다. 모든 도로의 거리는 1이다.
이 때 특정한 도시 X로부터 출발하여 도달할 수 있는 모든 도시 중에서, 최단 거리가 정확히 K인 모든 도시들의 번호를 출력하는 프로그램을 작성하시오. 또한 출발 도시 X에서 출발 도시 X로 가는 최단 거리는 항상 0이라고 가정한다.
예를 들어 N=4, K=2, X=1일 때 다음과 같이 그래프가 구성되어 있다고 가정하자.
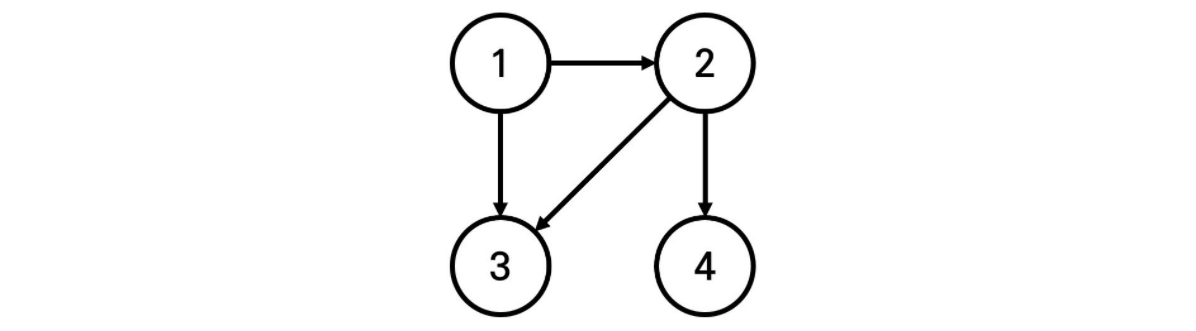
이 때 1번 도시에서 출발하여 도달할 수 있는 도시 중에서, 최단 거리가 2인 도시는 4번 도시 뿐이다. 2번과 3번 도시의 경우, 최단 거리가 1이기 때문에 출력하지 않는다.
입력
첫째 줄에 도시의 개수 N, 도로의 개수 M, 거리 정보 K, 출발 도시의 번호 X가 주어진다. (2 ≤ N ≤ 300,000, 1 ≤ M ≤ 1,000,000, 1 ≤ K ≤ 300,000, 1 ≤ X ≤ N) 둘째 줄부터 M개의 줄에 걸쳐서 두 개의 자연수 A, B가 공백을 기준으로 구분되어 주어진다. 이는 A번 도시에서 B번 도시로 이동하는 단방향 도로가 존재한다는 의미다. (1 ≤ A, B ≤ N) 단, A와 B는 서로 다른 자연수이다.
출력
X로부터 출발하여 도달할 수 있는 도시 중에서, 최단 거리가 K인 모든 도시의 번호를 한 줄에 하나씩 오름차순으로 출력한다.
이 때 도달할 수 있는 도시 중에서, 최단 거리가 K인 도시가 하나도 존재하지 않으면 -1을 출력한다.
예제 입력 1
4 4 2 1
1 2
1 3
2 3
2 4예제 출력 1
4예제 입력 2
4 3 2 1
1 2
1 3
1 4예제 출력 2
-1예제 입력 3
4 4 1 1
1 2
1 3
2 3
2 4예제 출력 3
2
3
📌 풀이
💬 Code
import sys, heapq
input = sys.stdin.readline
INF = float('inf')
def dijkstra(start):
q = []
heapq.heappush(q, (0, start))
distance[start] = 0
while q:
dist, now = heapq.heappop(q)
if dist > distance[now]:
continue
for i in graph[now]:
cost = dist + i[1]
if cost < distance[i[0]]:
distance[i[0]] = cost
heapq.heappush(q, (cost, i[0]))
n, m, k, start = map(int, input().split())
graph = [[] for _ in range(n+1)]
distance = [INF] * (n+1)
for _ in range(m):
a, b = map(int, input().split())
graph[a].append((b, 1))
dijkstra(start)
isNone = 1
for i in range(1, n+1):
if distance[i] == k:
isNone = 0
print(i)
if isNone:
print(-1)💡 Solution
BFS로도 풀 수 있는 문제지만 다익스트라를 배운 김에 다익스트라로 풀어보았습니다.